Using Pythagoras' Theorem on 3D Shapes

In this activity, we will look at using Pythagoras' theorem on 3D shapes.

Let's remind ourselves of the theory with an example:

a² + b² = c²

To find the hypotenuse of a triangle:

1. Square one side: 2² = 4²

2. Square the other side: 6² = 36²

3.  Add your answers together: 36 + 4 = 40² 

4. Square root your answer: √40 = 6.32 (to 2 decimal places)

Pythagoras in 3D

Now let's consider using this in 3D shapes instead of 2D.

Calculating a length is just the same as when working with a 2D triangle; the trick is being able to spot a right-angled triangle within the shape.

Let's look at this cuboid as an example:

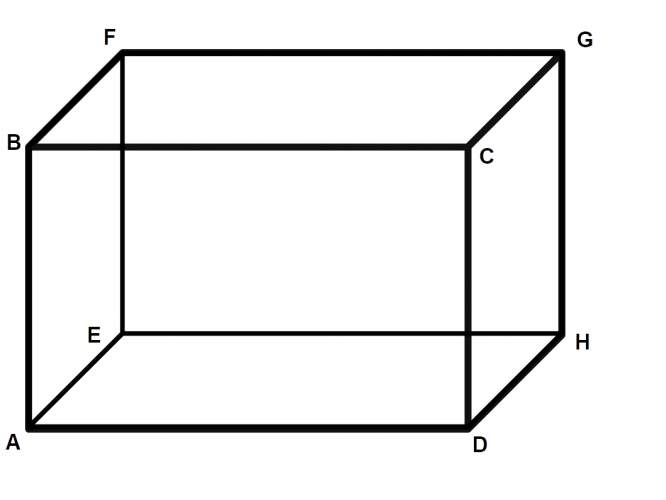
We can find any diagonal line across any face of a cube or cuboid, as the diagonal forms the hypotenuse of a right-angled triangle. 

For example:

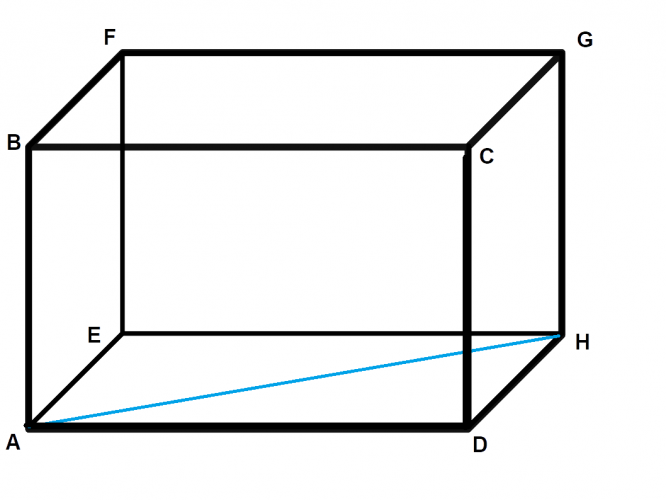
Triangle ADH is a right-angled triangle, and we can use a² + b² = c² to calculate length AH (the hypotenuse). 

Here is an overhead view of the base with our line drawn:

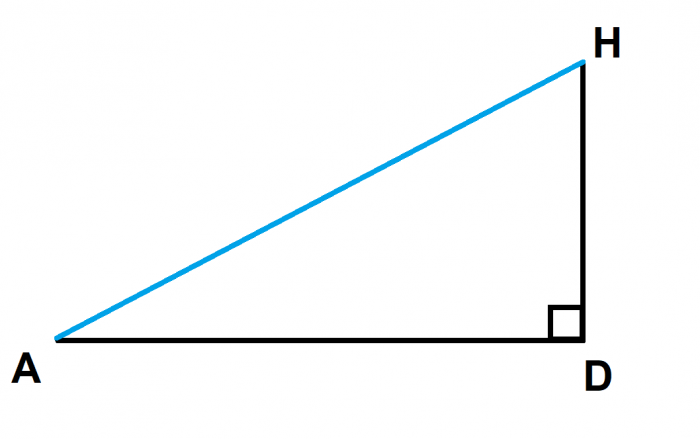
We can then take this into 3 dimensions by drawing another diagonal through the shape:

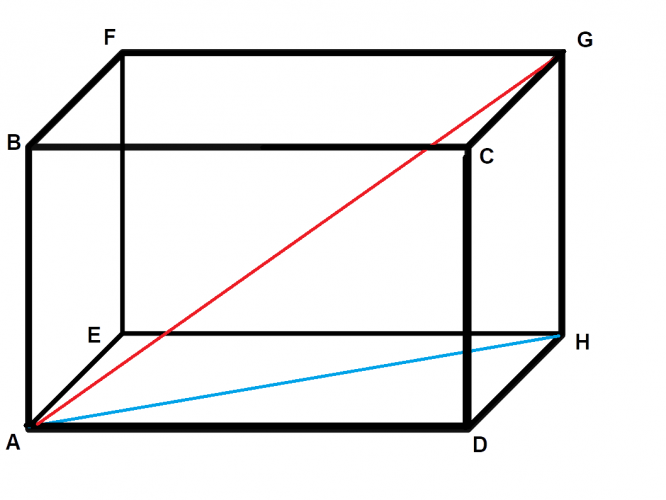
Here is a cross-section of the shape we have created.

We now have a new triangle, AGH, which extends from the bottom corner of the cuboid into the opposite top corner. Significantly, it is still a right-angled triangle, so we can continue to use a² + b² = c² to calculate the hypotenuse, AG. By doing this, we are using Pythagoras in 3D.

Example

Calculate length AG in this cube.

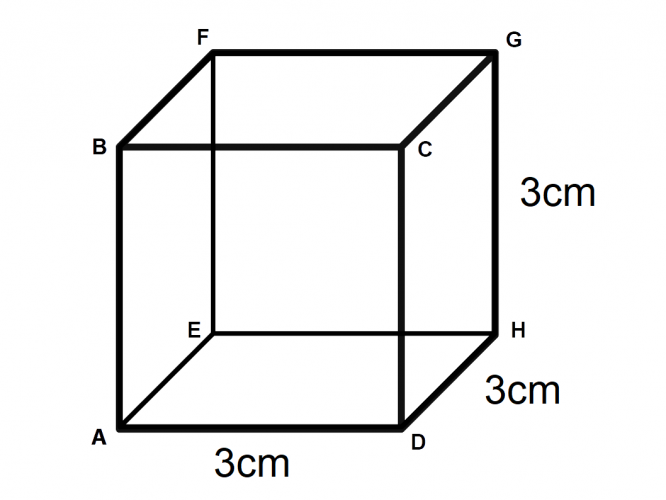
The first thing we can do is work out the diagonal across the base, AH:

a² + b² = c²

3² + 3² = AH²

AH² = 18 

AH = √18

As we will soon be squaring this answer, it is useful to leave the number in root form at this stage, rather than working with a decimal.

We can then use this length to work out the hypotenuse of triangle AGH:

a² + b² = c²

(√18)² + 3² = AG² 

AG² = 18 + 9 = 27

AG = √27 = 5.2 (1 d.p.)

Now that you have seen these examples, have a go at 10 questions to see if you can apply Pythagoras to 3D shapes.