Angles have various properties or facts which we can use to help us solve related problems.
In this activity, we will be investigating and utilising this fact:
Angles on a straight line will always add up to 180°.
It is important to note, this condition about the placement of the angles:
Angles have to be adjacent (next to each other) on the line.

This is incorrect as the angles are not next to each other.
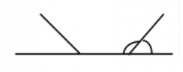
This is correct. The angles are adjacent.
Let's look at this information in practice in some examples now.
e.g. Find the missing angle in the diagram below.
We know that the sum of the angles on the line must add up to 180°.
Therefore, we can calculate the missing angle by subtracting the known angle from 180:
180° - 45° = 135°
That wasn't too tricky, was it?
Let's try another to check you have the rule down and know how to apply it accurately.
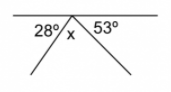
e.g. Find the angle x in the diagram below.
We might have been given two angles this time, but that is no bother, we just need to follow the same process through twice:
180° - 28° - 53° = 99°
Alternatively, we can add the angles given together first and then subtract this total from 180°:
28° + 53° = 81°
180° - 81° = 99°
Right then, let's put what we know into action now.
In this activity, we will use the key fact, that angles on a line always add to 180°, to find the value of unknown angles using numbers and algebra and solve problems involving collections of angles.