Solve Simultaneous Equations Graphically

In other activities, you have looked at how to solve simultaneous equations using algebraic methods. Sometimes you will be expected to use a graph to solve these equations, so let's quickly remind ourselves what simultaneous equations actually are.

Simultaneous equations are two equations that have the same values of x and y

If we consider how this links into graphs, we can draw the functions on a graph and find the points where x and y are the same. The solution to simultaneous equations will be the point where the two graphs intersect.

Example 1:

By using graphs, find the solution to the simultaneous equations 2x + 3y = 8 and 3x – y = 1

Step 1: Draw the two graphs on a single set of axes.

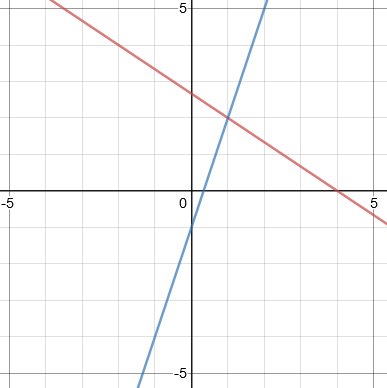
Step 2: Read off the coordinates where the two lines cross.

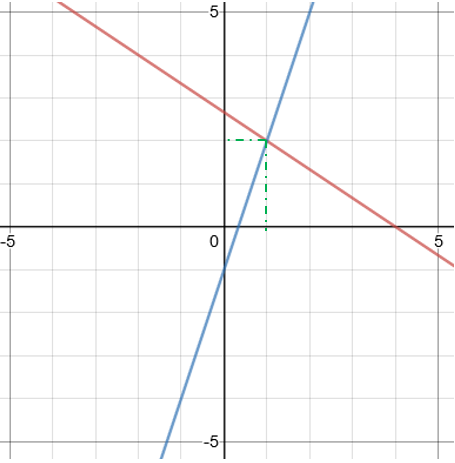
From the graph, we can see that the solutions to the equations are x = 1 and y = 2

Other graphs

Unfortunately, this topic isn’t limited to using linear graphs. You could also be expected to do this with quadratics and circles as well.

The good news is that the method to complete this is exactly the same, you’ll just could get more solutions.

Example 2:

By using graphs, find the solution to the simultaneous equations x² + y² = 25 and y = 2x + 1

Step 1: Draw the two graphs on a single set of axes.

Step 2: Read off the coordinates where the two lines cross.

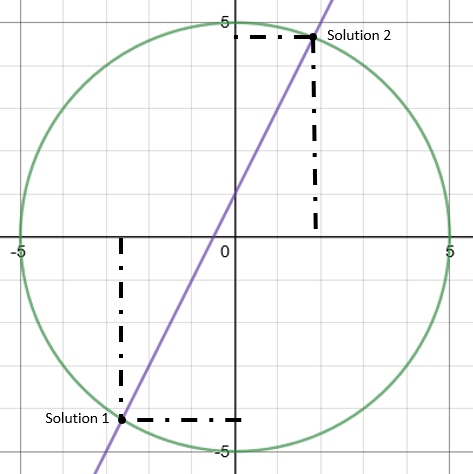
From this graph, we can see that the intersections are at (-2.6,-4.3) and (1.8,4.7)

This gives two sets of solutions:

x₁ = -2.6 and y₁ = -4.3

x₂ = 1.8 and y₂ = 4.7

Let's move on to some questions now.