Solve Problems Using Pythagoras' Theorem

In this activity, you will apply Pythagoras' theorem to various situations.

Let's recap the formula:

If we have a triangle with lengths a, b, and c:

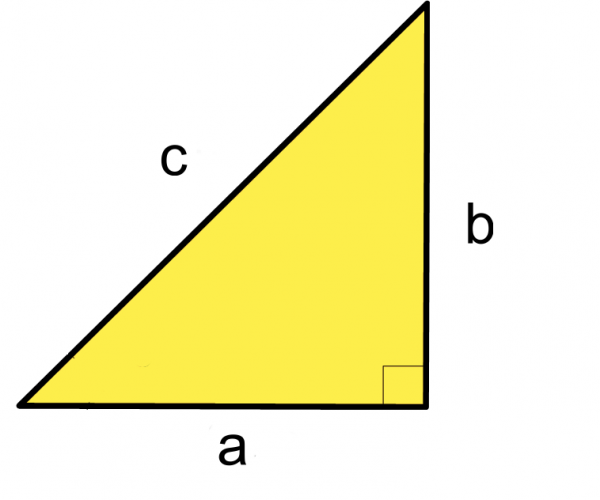
Pythagoras' theorem is:

a² + b² = c²

Remember this only works for right-angled triangles.

Example

To find the hypotenuse (longest side) of the triangle:

Step 1: Square both sides: 
10² = 100
3² = 9

Step 2: Add them:
100 + 9 = 109

Step 3: Square root:
√109 = 10.44 cm (to 2 decimal places)

To find a shorter side length:

Step 1: Square both sides: 
9² = 81
7² = 49

Step 2: Subtract them:
81 - 49 = 32

Step 3: Square root:
√32 = 5.66 (to 2 decimal places)

What if there isn't a triangle drawn for us?

This activity will focus on questions where you need to either spot a right-angled triangle within a shape, or make one using the information given.

For example:

I leave my house to go to the bus stop.

I walk 20 m due west and then walk another 30 m due north.

If I had taken the direct route how far would I have walked?

Draw the situation

We have been told that the person walks 20m west, followed by 30m north. We can put these lines together as shown:

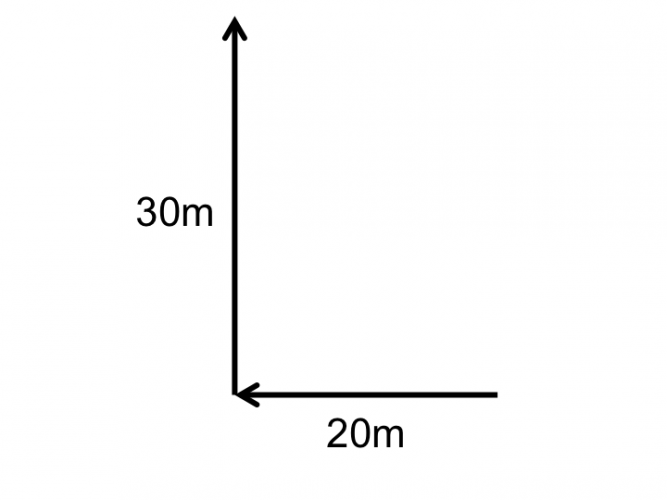
Now, let's join the shape up...

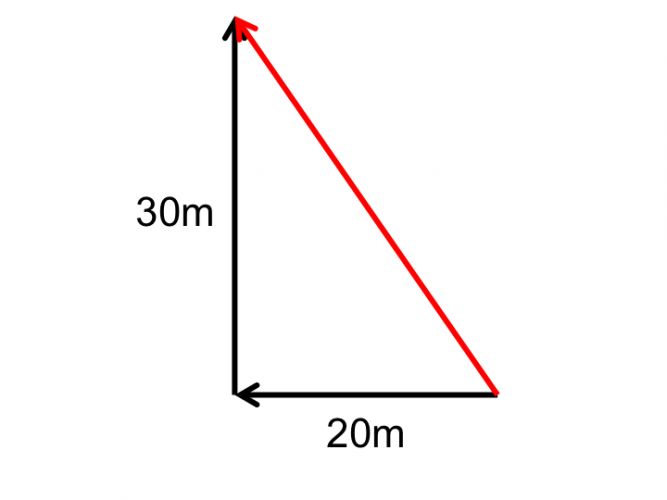
...And you can see a right-angled triangle has been formed! The direct route would be the diagonal (hypotenuse)

So, we use Pythagoras as follows:

20² = 400

30² = 900

400 + 900 = 1300

√1300 = 36.05 m (2 d.p.)

The key point is to always sketch the situation, or look to find a right angled triangle within a shape.

Have a go at this activity and see if you can use this skill.