What is rotational symmetry?
A shape has rotational symmetry when it still looks the same after some rotation of less than one full turn through 360°.
A shape's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same within one rotation.
Applied in geometric shapes
If we take a square and rotate it through a full turn, it will look exactly the same on four occasions: after a quarter turn, half turn, three-quarters of a turn and a full turn.
We call this rotational symmetry of order 4.
If we take a rectangle and rotate it through a full turn, it will look the same twice: after half a turn and a full turn.
We call this rotational symmetry of order 2.
If we take an isosceles triangle and rotate it through a full turn, it will look the same only once: after a full turn.
We call this rotational symmetry of order 1.
e.g. What order of rotational symmetry does this shape have?
If we rotated this shape through a full turn, we would reach this same image on three occasions: 1/3 of a turn, 2/3 of a turn and a full turn.
So this shape has rotation symmetry of order 3.
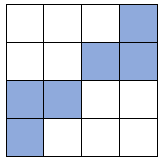
e.g. Which squares would we have to shade for this shape to have rotational symmetry of order 2?
'Order 2' means it would look the same twice within one full rotation of 360°.
If we divide the full turn (360°) by this, we find that it looks the same every 180°.
If we rotated the shape 180°, the shaded trio of squares would be in the bottom left corner instead, like this:
So this version of the square will have rotational symmetry to the order of 2.
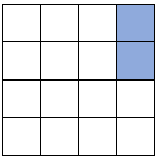
e.g. Which squares would we have to shade for this shape to have rotation symmetry of order 4?
'Order 4' means it would look the same four times within a full rotation.
If we divide the full turn (360°) by this, we find that it looks the same every 90°.
If we rotated the shape 90°, the shaded pair of squares would be in the bottom right corner.
If we rotated the shape another 90°, the shaded pair of squares would be in the bottom left corner.
If we rotated the shape a final 90°, the shaded pair of squares would be in the top left corner.
If we colour all these squares, our final image will look like this:
In this activity, we will recall and identify the rotational symmetry of common 2D shapes, plus locate squares in a grid to colour to create rotational symmetry to a specified order.