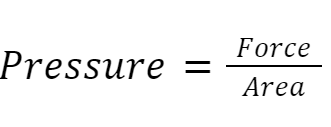Carry Out Calculations Involving Pressure

Imagine you went snowboarding. Even if you were stationary, you would not sink into the snow.

But, if you stood on snow, you might sink into it. That's because the pressure caused by your weight acting downwards would be greater. On a snowboard, your weight is distributed over a greater area, decreasing your pressure.

In this activity, we will be reviewing the link between pressure, force and area and practising using the pressure equation. 

First, let's define pressure. Pressure is a measure of how concentrated a force is - it is a force over a given area. The greater the pressure, the more concentrated the force.

We can calculate pressure using this equation:

When calculating pressure, the force is measured in Newtons (N). Typically, the area is measured in m² (although occasionally it is measured in cm²). 

Pressure is measured in Pascals (Pa), or Newtons per square metre (N/m²). We do sometimes measure pressure in N/cm², but that is less common. 

What if we had to calculate the force, using pressure and area? We would need to rearrange the formula.

To rearrange the original pressure formula, and make force the subject, we need to multiply both sides of the equation by area.

As you can see, the area terms on the right-hand side of the equation cancel out, leaving us with an equation for force.

Example 

A person stands on a snowboard and causes a downwards pressure of 1,750 Pa. The area of the snowboard is 0.4 m²

What is the force caused by the person?

Answer 

We need to start with the rearranged pressure equation. 

Force (N) = Pressure (Pa) × Area (m²)

Force (N) = 1,750 Pa × 0.4 m²

Force = 700 N

What if we had to calculate the area, using pressure and force? Once again, we would need to rearrange the formula.

Let's start this time with the force formula. Now, to make area the subject, we must divide both sides of the equation by pressure

Pressure cancels out on the right-hand side, and we are left with this equation for area. 

Example 

A tennis racket has a weight of 3 Newtons, and is laying on the ground. It causes a pressure of 30 Pa. 

What is the area of the racket?

Answer 

Let's use our new equation for area.

Area (m^₂) = Force (N) ÷ Pressure (Pa)

Area (m²) = 3 N ÷ 30 Pa

Area = 0.1 m²

It is always important to check units in calculation questions. For example, what if the pressure was listed as 3 kPa? What would that mean?

kPa means kilo Pascals, and 'kilo' means 1,000. So, 3 kPa means the same thing as 3,000 Pa.

We need to use 3,000 Pa in any calculations we do, or we might get the wrong answer!

To convert from kPa to Pa, multiply by 1,000.

To convert from kN to N, multiply by 1,000. 

Let's get started.