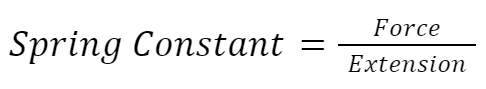Use Hooke's Law to Carry Out Calculations

Imagine pulling on a spring. When you apply a force, it will stretch and extend. In fact, the amount of force will affect the extension of the spring. 

If you double the force on the spring, the extension will double. Why? Because springs are an example of a material that follows Hooke's Law. Let's learn about Hooke's Law, and practise using it in calculations. 

Hooke's Law states that, for certain materials, the extension of the material is directly proportional to the force acting on the material. So, if we double the force, we double the extension. If we triple the force, we triple the extension.

Example

Someone applies 3 Newtons of force when they stretch a spring. The spring extends by 4 cm. What would the extension of the spring be if a force of 6 Newtons was applied instead?

Answer 

In this situation, the spring is experiencing double the force, so it must extend by double the amount. 

4 cm × 2 = 8 cm

We can express Hooke's Law, just like many other proportional relationships, with an equation. 

Force = Spring Constant × Extension

Or, simplified, 

F = k × e

F stands for force and is measured in Newtons (N)

k stands for spring constant and is measured in Newtons per metre (N/m)

e stands for extension and is measured in metres.

What does 'spring constant' mean?

The spring constant is a measure of how stretchy a material is. The spring constant is a number that is different for each material.

The greater the spring constant, the harder it is to stretch a material. The smaller the spring constant, the easier it is to stretch. 

Example

 A material has a spring constant of 0.6 N/m. It has an extension of 0.2 m. What is the force on the material?

Answer

First, we write down the equation. Then, we substitute in the values that we know. 

F = k × e

F = 0.6 N/m × 0.2 m = 0.12 N

We can also rearrange the equation for Hooke's law, for situations when we want to calculate the spring constant, or the extension, instead. 

Example

 What is the spring constant for a stretchy material, if it experiences a force of 2.5 Newtons, and extends by 8 cm?

Answer

We actually have to convert the extension from cm to m before we do anything else!

8 cm ÷ 100 = 0.08 m

Now we can use the rearranged equation. 

k = 2.5 N ÷ 0.08 m = 31.25 N/m

Now that we have seen Hooke's Law in action, let's try some practice questions!