BACK TO WORKSHEETS
It is possible to work out the gradient of a straight line from the coordinates of any two points which lie on the line, either by drawing the line or simply by subtracting and dividing coordinates.
The rule to remember is:
The gradient of a line = y-step ÷ x-step
Example
Find the gradient of the straight line that passes through (2, 5) and (5, 9)
Answer 1
Let's look at the line drawn on a set of x-y coordinate axes.
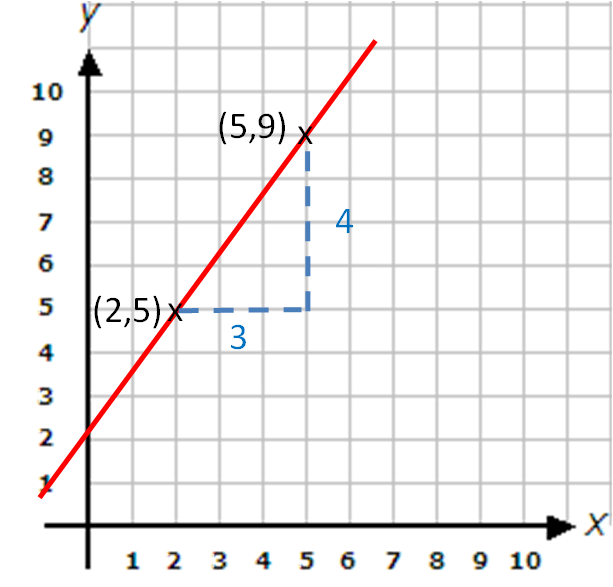
The vertical part of the step (y-step) = 4
The horizontal part of the step (x-step) = 3
The gradient of the line = y=step ÷ x-step = 4 ÷ 3 = 4/3
Answer 2
It is possible to work out the gradient without drawing the line.
Look at the coordinates of the two points (2, 5) and (5, 9).
We can get the y-step by subtracting the y-coordinates.
y-step = 9 - 5 = 4
In the same order, we get the x-step by subtracting the x-coordinates:
x-step = 5 - 2 = 3
The gradient of the line = y-step ÷ x-step = 4 ÷ 3 = 4/3
NB: We could have worked out 5 - 9 = -4 and 2 - 5 = -3 but -4 ÷ -3 = 4 ÷ 3
Want a bit more help with this before you begin? Why not watch this short video?
