Understand Long Division Leaving Remainders as Fractions

In this activity, we will divide numbers with up to four digits by two-digit numbers using long division.

There will be remainders which should be written as fractions.

Let's look at   1986 ÷ 15

We start by setting out the calculation as usual, like this, and then start dividing.

First, we divide 19 ÷ 15 = 1 rem 4.

(Remember that 1 × 15 = 15 and so the remainder is 19 - 15 = 4.)

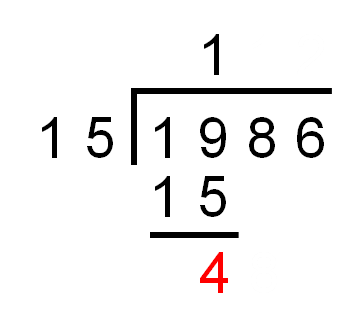
Bring the 8 down next to the 4.

Then, we divide 48 ÷ 15 = 3 rem 3.

(Remember that 3 × 15 = 45 and so the remainder is 48 - 45 = 3.)

Bring the 6 down next to the 3.

Now we divide 36 ÷ 15 = 2 rem 6.

(Remember that 2 × 15 = 30 and so the remainder is 36 - 30 = 6.)

The final remainder is 6, but we want to write this as a fraction.

We are dividing by 15, so a remainder of 6 is actually the fraction 6/15.

To reduce this fraction to its lowest terms, we look for the highest number that goes into 6 and 15.

This will be 3 because 2 × 3 = 6 and 5 × 3 = 15.

So, we divide the top and the bottom numbers by the magic number 3 to get 2 and 5.

6/15 = 2/5

We have shown that 1986 ÷ 15 = 132 and 2/5

Does that make sense?

Let's get started then! You can look at this example any time you want to by clicking on the red help button on the screen.