Distinguish Between Dependent and Independent Events

What does it mean (in plain English) when one thing is dependent on another?

It means that thing depends on the other, i.e. changes in one affect the other!

Similarly, in maths, dependent events means that the probability of one event depends on the outcome of the other.

For example, let's say we have 6 cherry sweets and 9 lemon sweets in a bag and two sweets are drawn at random.

Then the probabilities of getting cherry or lemon for the second sweet depends on what flavour we drew as the first one!

If the first sweet was cherry, then now we have only 6 - 1 = 5 cherry sweets - which affects the probability!

On the other hand, independent events don't affect each other: the probability of something happening doesn't change based on the outcome of the previous event.

In a tree diagram, we can recognise that we have independent events by looking at the set of branches under each other:

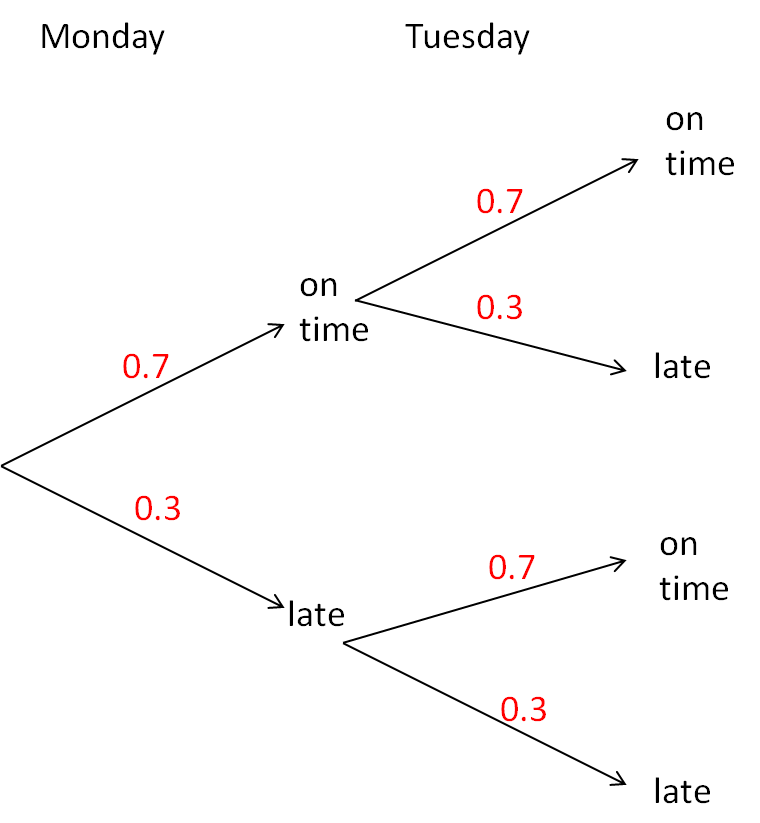
Here, we can see that the probabilities that a train will be on time or late on Tuesday are the same whether the train was late on Monday or not!

So 'being late on Tuesday' and 'being late on Monday' are independent.

Dependent events have different branches under each other in a tree diagram:

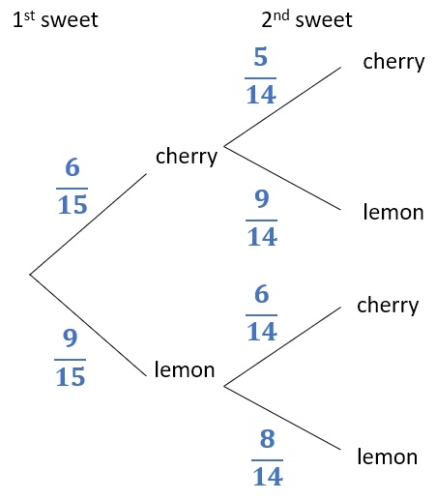
We can see that the probability of getting cherry given that we have already picked cherry is 5/14.

Whereas the probability of getting cherry given that we have already picked lemon is 6/14.

So 'getting cherry for the second sweet' depends on what flavour we got for the first sweet, so we have dependent events.

Finally, here we are talking about the probability of something given something else - does that ring any bells?

That is our conditional probability!

For example, the probability of getting cherry given that we have already got cherry has the condition of getting cherry for the first sweet!

'Given' is denoted by a vertical line |.

So if we call getting cherry C and getting lemon L, then we have:

- the probability of getting cherry given we have already got cherry is P(C | C) = 5/14

- the probability of getting cherry given we have already got lemon is P(C | L) = 6/14

Since P(C | C) ≠ P(C | L), the events are dependent.

Ready to put this all into practice?