When you are given a list of numbers, how can you find the median (i.e. the middle number)?
2, 5, 1, 3, 8, 6, 3

We first put them in order, from the smallest to the largest:
1, 2, 3, 3, 5, 6, 8
Then cross one from each side until we have only one left in the middle:
1, 2, 3, 3, 5, 6, 8
1, 2, 3, 3, 5, 6, 8
1, 2, 3, 3, 5, 6, 8
The number in the middle we are left with is 3, so that is the median!
That is pretty straightforward, right?

But what if now, we had the data grouped into a table like this (i.e. grouped data)?
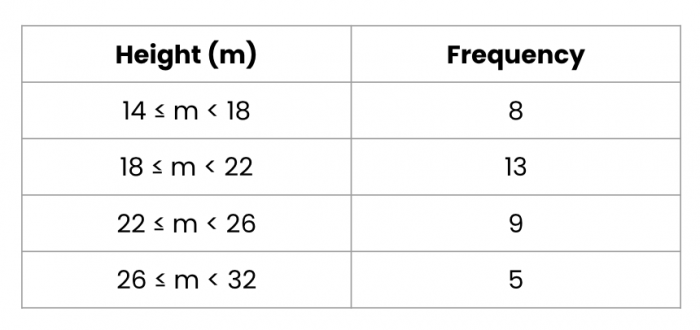
First things first, let's go over what this table actually means!
In the first line, we have m between 14 and 18 with a frequency of 8.
That means there are 8 heights in the data that are between 14 and 18.
We don't know what exactly those 8 numbers are: they could be eight 16s, three 14.5s and five 17s or any other combination of numbers between 14-18 you can think of!
How could we find the median from such a table?
Well, if we think back to our first example (numbers 1, 2, 3, 3, 5, 6, 8), there were 7 numbers altogether and the median was the 4th number. Which was 3.
How could we get 4 using 7?
Well, 4 is half of 8 - and that is 1 more than 7!
The position of the median within the ordered numbers is therefore:
(How many numbers we have + 1) divided by 2
Let's verify we've got that right:
(7 + 1) ÷ 2 = 8 ÷ 2 = 4
The median should be in the 4th place within 1, 2, 3, 3, 5, 6, 8.
And indeed, our median of 3 was in the 4th place!
Coming back to our lovely table:

To find the median, we first need to find which position it occupies.
For that, we need to know how many data points we have.
Where in the table is that? The frequency column!
We have 8 data points between 14-18 m, 13 data points between 18-22 m and so on.
So the total number of data points (i.e. how many numbers we have) will be the sum of all the frequencies!
So we have 8 + 13 + 9 + 5 = 35 data points.
The position of the median is then this 35, add 1 and all of that divided by 2:
(35 + 1) ÷ 2 = 36 ÷ 2 = 18
So is 18 the median?
No! We need to be careful here, 18 is just the position of the median,
i.e. the median is in the 18th position.
So where is that?

Looking back at our table, there are 8 numbers between 14 m and 18 m. We just don't know what they actually are.
These are the position of the first 8 numbers, i.e.: 1st, 2nd, 3rd, 4th, 5th, 6th, 7th and 8th
Then there are 13 numbers between 18 m and 22 m.
These are the next 13 numbers (after the 8th number from before), i.e.:
9th, 10th, 11th, 12th, 13th, 14th, 15th, 16th, 17th, 18th, 19th, 20th and 21st
We can see that the 18th number is there!
That is our median!
We can therefore say that 18≤m<22 is the class (or the interval) that contains the median.
So now you can find which class the median is in!

Don't worry if this seems tricky - remember that you can look back at this introduction at ny point by clicking on the red help button on the screen.
Let's have a go!







