Calculate Probabilities of Complementary Events

What is the probability that it's going to rain or not rain today?

Well, it can either rain or it can not rain - there's no other option!

So it's certain it will rain or not rain today.

What is the probability when something is 100% likely to happen?
It's 1!

But now, what if we knew that the probability of it raining today is 0.3 (or 3/10 if you prefer fractions)?

How could we use it to calculate the probability of not raining today?

Well, we know that together the probability of raining and the probability of not raining make 1, since one of them has to happen.

So, P (not raining) = 1 - P (raining)

which gives us  1 - 0.3 = 0.7

We call something happening and that event not happening complementary events.

For example, not raining today is a complementary event to (or a complement of) it raining today because it complements it (together they make a complete 1).

Probabilities of complementary events always add up to 1:

P (A) + P (not A) = 1

So the probability of something not happening can always be calculated by:

P (not A) = 1 - P (A)

It does seem confusing, doesn't it, but it will become clearer with practice.

Let's have a look at an example!

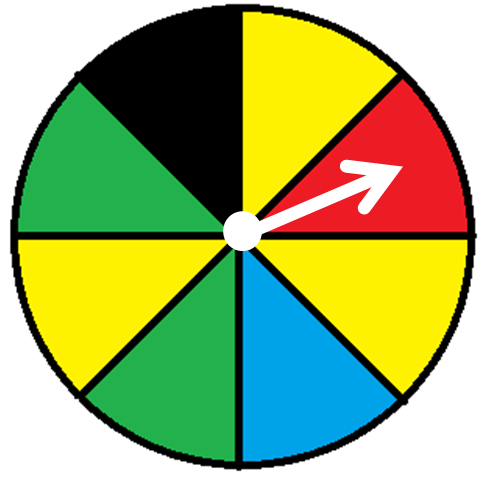
There are three yellow sections out of eight on the spinner, so the probability of the spinner landing on yellow is 3/8.

The probability of the spinner not landing on yellow is 1 - 3/8 = 5/8.

If the probability of you getting all the questions correct is 9/10, what's the probability that you don't get them all correct?

Could it be 1 - 9/10, which is 1/10?!

Yay! Let's give it a go!