Lost again?
Not to worry! The GPS on your phone can help you find your way.
GPS uses angles, including exterior angles, to help calculate and create directions.
The mathematics used in GPS is quite complex, but we can learn about some of the basics to get us thinking a bit more like a GPS system.
Let's start by considering what we need to know about exterior angles around points and polygons.
Here is a polygon with its exterior angles highlighted:
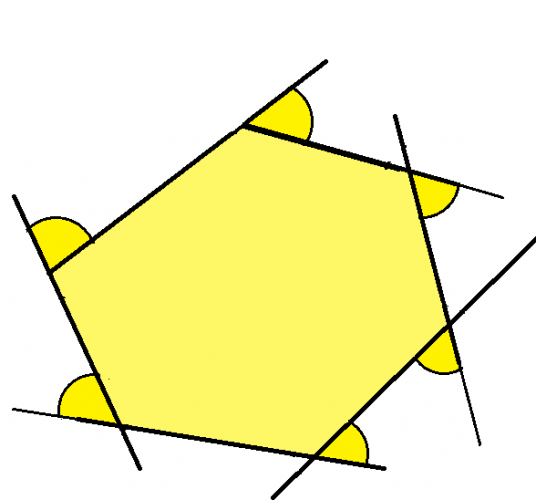
If we connect them all together, they always fit perfectly around a point:

This means that the exterior angles of any polygon add up to 360°.
How to calculate the exterior angle of a regular polygon
A regular polygon's sides are all the same length (e.g. an equilateral triangle). It also means all the angles around the shape are equal.
Let's look at an example:
Find the exterior angle of a regular pentagon.

Because the exterior angles of a polygon will fit around a point, and we know that angles around a point add up to 360°, we just use this fact, along with the number of sides of the polygon, to calculate any exterior angle. So:
360° ÷ number of sides = value of external angle
In this case:
360° ÷ 5 = 72°
Hopefully, now you won't get lost!
In this activity, we will calculate the exterior or external angles of polygons with a variety of different sides by applying the rule that all exterior angles in a polygon will add up to 360°.








