Apply Trigonometry Knowledge to 3D Shapes

Questions

How can this mountaineer draw an accurate map?

How did sailors navigate before GPS?

How can computers rotate images so that they can be viewed from many different directions?

Answer

They look at angles and sides of triangles and make connections between them.

This is called trigonometry.   A lot of the time, trigonometry is applied in 3D, and this is the skill that you will practise in this activity.

Trigonometry ratios - recap

You should be able to recall, for any right-angled triangle:

sin x = O/H

cos x = A/H

tan x = O/A

When you are dealing with a 3D shape, you will need to draw a right-angled triangle inside it and identify the relevant lengths to apply sin, cos, or tan.

Example

Shown below is cuboid ABCDEFGH.

AB = 20cm
BD = 4cm
DH = 5cm

Calculate angle ABE.

Step 1: Sketch the shape and label the lengths if they are not already written down.

We were given AB = 20cm, BD = 4cm, and DH = 5cm, so we should identify these sides and write the correct lengths. 

Step 2: Draw a right-angled triangle onto the shape that contains the angle you want to find.

In this case, we want angle ABE, so our triangle must consist of points A, B, and E.

Step 3: Re-draw the triangle in 2D and use the correct trig ratio to solve.

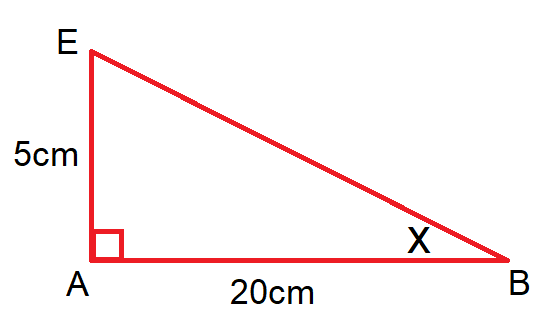
The question seems much more simple if we just look at our triangle separately.

We want angle ABE, labelled x. The adjacent length = 20cm and the opposite length = 5cm.

We must therefore use tan to solve.

tan x = O/A

tan x = 5/20 = 0.25

x = tan^-1 (0.25)

x = 14.0º (1 d.p.)

Now that you have seen a worked example, have a go at calculating angles in other 3D shapes. Make sure you sketch the shape, identify the triangle you need, and use the correct trig ratio.